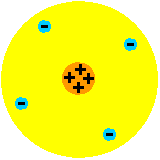Cząsteczki wielu substancji maja kształt symetryczny. Na rysunku z prawej strony kulka mająca ładunek dodatni przedstawia jądro atomu wchodzącego w skład cząsteczki, a kula naładowana ujemnie wyobraża powłoki elektronowe tych atomów. Atomy znajdujące się blisko siebie oddziaływują wzajemnie. Przy odległościach między sobą rzędu 10^-9 m następuje przesuwanie i deformowanie się chmur elektronowych wewnątrz atomów (rysunek poniżej) w wyniku czego powstają dipole (układ dwóch ładunków o jednakowych wartościach ale przeciwnych znakach) i atomy przyciągają się siłami elektrostatycznymi. Siły te nazywamy siłami Van der Waalsa. Jest proces analogiczny do elektryzowania przez indukcję papierków przez 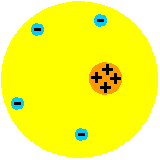naelektryzowaną laskę, a następnie ich przyciąganie elektrostatyczne. Ładunki różnoimienne są bliżej niż różnoimienne i dominuje przyciąganie. Siły Van der Waalsa są krótkozasięgowe, jej wartość jest odwrotnie proporcjonalna do siódmej potęgi odległości między atomami.
Przy odległościach między atomami rzędu 10^-10 m (tej samej co rozmiary atomów) chmury elektronowe różnych atomów nakładają się na siebie i sytuacja się komplikuje. Oddziaływanie zależy od tego, z jakimi atomami mamy do czynienia. Niektóre atomy mogą wchodzić w reakcje chemiczne i charakter tych sił jest przyciągający. Między atomami nie wchodzącymi w reakcje chemiczne siły oddziaływania na małych odległościach mają charakter silnie odpychający. Siła ta jeszcze bardziej zależy od odległości i jest odwrotnie proporcjonalna do potęgi większej niż osiem odległości między atomami, czyli jest jeszcze bardziej krótkozasięgowa.

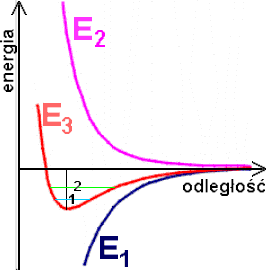
Zależność energii potencjalnej oddziaływania atomów od odległości E1 - energia potencjalna związana z przyciąganiem, E2 - energia potencjalna wynikająca z odpychania, E3 - energia całkowita

Znając charakter sił międzycząsteczkowych można narysować wykres energii oddziaływania międzycząsteczkowego - tak zwaną krzywą energii potencjalnej. Na wykresie obok E₁ przedstawia energię potencjalną związaną z przyciąganiem (siły Van der Waalsa), E₂ pokazuje energię potencjalną wynikającą z odpychania, natomiast E₃ energię całkowitą. Trzeba zauważyć, że wykres energii całkowitej nie jest symetryczny i energia całkowita ma minimum. Zgodnie z ogólną zasadą każdy układ przyjmuje taki stan aby jego energia była jak najmniejsza. Atomy w ciele stałym lub cieczy będą się więc znajdować w takiej odległości aby energia całkowita była minimalna. Ale atomy ciała stałego lub cieczy wykonują drgania. Ponieważ zależność energii całkowitej od odległości nie jest symetryczna to średnia odległość nie znajduje się w minimum energii lecz jest nieco większa. Czym wyższa jest temperatura tym większa zmiana energii i średnia odległość znajdująca się na środku między położeniem minimalnym i maksymalnym rośnie. Na wykresie 1 pokazuje zmiany energii w niższej temperaturze a 2 w wyższej. Numerki umieszczone są w średniej odległości. Po podgrzaniu substancji średnie odległości rosną, więc ciało zwiększa swoje rozmiary.
Powyższy opis jest bardzo uproszczony ponieważ pełna teoria sił międzycząsteczkowych może być zbudowana tylko na bazie mechaniki kwantowej (ruch elektronów w atomie traktujemy jako falocząstki czyli cząstki z uwzględnieniem ich właściwości falowych). W analizie należy uwzględnić fakt, że każda cząsteczka oddziałuje z wieloma cząsteczkami równocześnie i w ciałach stałych występują różne typy wiązań krystalicznych. Wykres może być nieco inny w różnych przypadkach ale zawsze występuje minimum energii i wykres jest niesymetryczny.
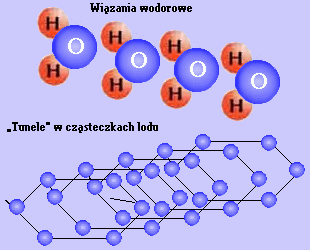Powyższy model nie potrafi wytłumaczyć anomalnych właściwości wody i niektórych innych cieczy. W zakresie od 0°C do 4°C objętość wody maleje przy wzroście temperatury. Wynika to z budowy wody. Cząsteczki wody nie mają symetrii sferycznej i oddziaływanie między nimi zależy nie tylko od odległości, lecz również od kierunku pod jakim są one ustawione względem siebie. Minimalnej energii potencjalnej układu cząsteczek odpowiada ściśle określone ustawienie ich kierunków. Takie właśnie uporządkowanie charakteryzuje sieć krystaliczna lodu. Średnia odległość między cząsteczkami jest wówczas nieco większa niż wtedy, gdy cząsteczki ustawione są chaotycznie. W wodzie w niskich temperaturach część cząsteczek tworzy uporządkowane zespoły, pozostałe są jednak ustawione chaotycznie. W miarę wzrostu temperatury liczba uporządkowanych zespołów maleje. Zachodzą więc dwa konkurencyjne procesy: rozpad uporządkowanych zespołów prowadzi do zmniejszenia średniej odległości między cząsteczkami, zaś wzrost amplitudy drgań prowadzi do zwiększenia tej odległości. Dopóki temperatura wody nie przekracza 4°C, decydującą rolę odgrywa pierwszy proces. W temperaturach wyższych od 4°C przeważa drugi proces i woda zachowuje się jak normalna ciecz.
Ilościowo rozszerzalność liniową ciał stałych charakteryzuje się podając dla danej substancji liniowy współczynnik rozszerzalności cieplnej (podaje on o jaką część długości początkowej zwiększa się długość ciała stałego gdy temperatura wzrasta o 1°C). W przypadku ciał izotropowych (mających jednakowe własności we wszystkich kierunkach) liniowy współczynnik rozszerzalności cieplnej jest taki sam we wszystkich kierunkach. Dla scharakteryzowania własność ciała anizotropowego (różne własności w różnych kierunkach) trzeba znać wartości liniowego współczynnika rozszerzalności cieplnej w dwóch (w przypadku kryształów jednoosiowych) lub trzech (w przypadku kryształów dwuosiowych) odpowiednich kierunkach. O zmianie objętości substancji informuje objętościowy współczynnik rozszerzalności cieplnej (określa on o jaką część objętości początkowej zwiększa się objętość substancji gdy temperatura wzrasta o 1°C). Jego wartość jest trzykrotnie większa od współczynnika liniowego.
Zjawisko rozszerzalności trzeba uwzględnić we wszelkich pracach inżynierskich, gdyż elementy konstrukcyjne mają inne rozmiary latem i zimą i znalazło wykorzystanie w wielu przyrządach. Przykładowo rozszerzalność cieczy (najczęściej zabarwionego alkoholu lub rtęci) wykorzystano w termometrach cieczowych.

Przerwy dylatacyjne w konstrukcji mostu

Stalowe przęsła mostu mogą być latem nawet o pół metra dłuższe niż zimą. Stosuje się wtedy stalowe "grzebienie", za których pomocą łączy się poszczególne części nawierzchni mostu. Nie przyczepia się też mostu sztywno do podłoża, lecz pod jednym z końców przęsła umieszcza stalowe walce, po których ten koniec może się toczyć. taki ruch umożliwiają przerwy dylatacyjne (dylatacja znaczy rozszerzanie). Budując drogę z betonową nawierzchnią, zostawia się szczeliny aby beton miał miejsce na rozszerzanie się w upalne dni. Napowietrzne przewody telefoniczne lub energetyczne są latem zawieszane luźno, aby się nie zerwały, kiedy będzie zimno i skurczą się. Linie energetyczne trakcji kolejowych i tramwajowych muszą być odpowiednio naciągnięte aby rozszerzalność nie zmieniała wysokości na której wiszą. Szklarz podczas wprawiania szyby zimą musi zostawić wolne miejsce w ramie okna aby szyby mogły się swobodnie zwiększać swoje rozmiary. Inaczej podczas wzrostu temperatury popękają Oczywiście zimą przerwy muszą być większe, a latem mniejsze. Linie ciepłownicze doprowadzające wodę na powierzchni ziemi nie są proste. Wykonuje się specjalnie kolana (patrz zdjęcie wyżej). Gdy rury rozszerzają się lub kurczą to zmieniają swoje rozmiary i przesuwają się na zagięciach i nie następuje ich wyginanie lub pękanie.

Przerwy dylatacyjne między szynami

Szyny kolejowe i tramwajowe łączy się ze sobą, zostawiając pomiędzy kolejnymi odcinkami przerwy dylatacyjne. Podczas jazdy pociągiem słychać charakterystyczne stukanie kół w miejscach przerw w szynach. Stalowa szyna o długości 100m w gorący dzień może być dłuższe o 5 cm niż w zimie. Obecnie aby uniknąć stukania stosuje się ukośne nacięcia na szynach.
Każdy metal rozszerza się inaczej. Element wykonany z dwóch metali różniących się rozszerzalnością cieplną nazywamy bimetalem. Po podgrzaniu bimetal wygina się ponieważ jeden z metali bardziej wydłuża się niż drugi. Wykorzystuje się to

Czujnik automatycznego regulowania od żelazka

produkcji czujników automatycznego regulowania temperatury. Czujniki te stosuje się między innymi w pralkach, lodówkach, żelazkach, kuchenkach elektrycznych. W piecykach gazowych czujnik odcina dopływ gazu gdy zgaśnie świeczka.
Pracę czujnika przedstawiamy na przykładzie żelazka. Czujnik włącza prąd w grzejniku żelazka, gdy jego temperatura osiągnie zadaną wartość. Gdy bimetaliczny pasek nagrzeje się, jego wygięcie sprawi, że obwód elektryczny zostanie przerwany. Po krótkim czasie, gdy pasek ostygnie obwód zostanie zamknięty i grzałka ponownie rozgrzeje żelazko.

Literatura:
Jan Blinowski, Jarosław Trylski, Fizyka dla kandydatów na wyższe uczelnie,
Podręcznik dla gimnazjum wydawnictwa Nowa Era - moduł 1.

---

« Poprzednia