|
| Start |
| Nauczyciele |
| Nauczanie |
| Konkursy |
| Ciekawostki |
| Aktualności |
| Astronomia |
| Struktura materii |
| Doświadczenia domowe |
| Testy z fizyki |
| Spis treści i wyszukiwarka |
Odkrycia
Drutem kwantowym nazywamy strukturę, w której elektrony poruszają się tylko w
jednym kierunku, a ruch w pozostałych kierunkach jest niemożliwy (mówimy, że
ruch jest skwantowany w tych kierunkach). Elektron tutaj porusza się w
przestrzeni jednowymiarowej. Elektrony w drucie kwantowym tworzą gaz
jednowymiarowy. Analogią (z makroświata-"świata dużych cząstek") do ruchu
elektronu w drucie kwantowym jest np. ruch lokomotywy po idealnie prostym torze
kolejowym (ruch tylko w kierunku X). Jeśli teraz długość toru kolejowego jest
równa odległości między skrajnymi osiami i lokomotywa nie może wykonywać ruchu w
żadnym kierunku, to zostanie uwięziona w swiecie zerowymiarowym - analogia do
kropki kwantowej. A więc, ograniczając ruch elektronu uniemożliwiamy mu
wykonywanie ruchu w pozostałym - trzecim kierunku i elektron zostaje uwięziony w
kropce kwantowej. Elektrony uwięzione w kropce kwantowej stanowią
zerowymiarowy gaz elektronowy. Aby zbudować kropke kwantową należy tylko
ograniczyć ruch elektronu we wszystkich trzech kierunkach wiążąc je w
trójwymiarowym pudle potencjału o zadanym kształcie. A teraz, gdy już wiemy czym
są tytułowe dziwadła kwantowe możemy zastanowić się w jaki sposób można je
otrzymać. Ograniczymy się do samej idei uzyskiwania drutów i kropek kwantowych
bez opisu technologii wytwarzania tych struktur.

Mikroświat ma swoje prawa, którymi się rządzi i fizycy nauczyli
się opisywać go za pomocą mechaniki kwantowej. Jeśli spróbujemy wyobrazić sobie
kryształ, to jawi nam się przed oczyma układ idealnie uporządkowanych w rzędach
odległych od siebie o kilka angstremów (1 angstrem to 10-10 m)
atomów, pomiędzy którymi może poruszać się elektron. Jeśli kryształ jest
idealny, czyli atomy znajdują się na swoich miejscach i nie ma obcych atomów
(zanieczyszczeń), to okazuje się, że ruch elektronu jest ruchem swobodnym (tak
jakby nie było tych wszystkich atomów), z tym tylko, iż jego masa ulega istotnej
zmianie. Zatem w krysztale idealnym elektron może być opisany jako cząstka
materialna o zmienionej (w stosunku do elektronu swobodnego w próżni) masie,
swobodnie poruszająca się w trzech wymiarach. Jest to pełna analogia do kulki
poruszającej się swobodnie w trójwymiarowej przestrzeni. Jeśli pozostaniemy przy
analogii kulki w trójwymiarowej przestrzeni, rodzi się pytanie: czy istnieje
metoda ograniczenia jej swobodnego ruchu do dwu wymiarów.Umieśćmy więc kulkę na
idealnie płaskim stole i przykryjmy ją od góry takim samym stołem, aby ruch kulki
mógł odbywać się tylko w płaszczyźnie stołu (kulka może swobodnie zmieniać
kierunek X i Y, natomiast ruch w kierunku Z-owym jest zabroniony).Dla swobodnego
elektronu w krysztale takimi ogranicznikami są bariery potencjału. Tego rodzaju
"ściany potencjału", wywołane zewnętrznymi czynnikami, elektron pokonuje wtedy,
gdy istotnie zwiększy swoją energię. Jeśli takie ściany ograniczają ruch
elektronu wzdłuż osi Z (zarówno w górę, jak i w dół), to swobodny ruch
dopuszczalny jest jedynie w płaszczyźnie X, Y (rys. 1).
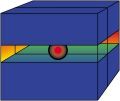
Rys. 1. Elektron uwięziony pomiędzy dwiema barierami potencjału Jak praktycznie zrealizować barierę potencjału dla elektronu poruszającego się w krysztale? Odpowiedź na to pytanie wcale nie jest prosta i wymaga głębokiej znajomości mechaniki kwantowej. Wyobraźmy sobie pary kryształów A i B o identycznej strukturze krystalicznej i niemal takiej samej stałej sieci (odległości między najbliższymi atomami na płaszczyźnie krystalicznej), z których można wykonać "kanapkę" BAB (analogia z kanapką jest oczywista: dwie kromki chleba, pomiędzy którymi znajduje się plasterek szynki).
Odpowiednio dobierając kryształy A i B, można uzyskać efekt, którego poszukiwaliśmy: swobodne elektrony znajdujące się w warstwie A, aby przedostać się do którejś z warstw B, napotykają barierę potencjału, do pokonania której potrzebują dodatkowej znacznej energii z zewnątrz. Tak długo, jak energia taka nie zostanie im dostarczona w warstwie A, są w niej uwięzione. Jeśli dodatkowo warstwa A jest bardzo cienka (około 100 Å), to jak już uprzednio mówiliśmy ich ruch skierowany prostopadle do warstwy jest niemożliwy, natomiast pozostaje nadal swobodny w płaszczyźnie warstwy. Można zaproponować wiele par kryształów A i B, które mogą być użyte do wytworzenia elektronów ograniczonych do dwóch wymiarów, czyli tzw. dwuwymiarowego gazu elektronowego. Obecnie najlepiej zbadanym układem jest GaAs jako warstwa A i kryształ mieszany Ga0.8Al0.2As jako warstwa B. Dwuwymiarowy gaz elektronowy uwięziony zostaje w cienkiej (około 100 Å) warstwie GaAs. 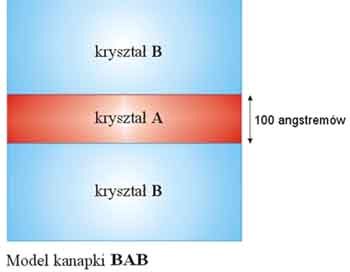
W sposób oczywisty nasuwa się pytanie, czy, wykorzystując opisane techniki, można wytworzyć drut kwantowy - strukturę, w której elektrony poruszać się będą mogły tylko wzdłuż jednego kierunku? Zatem czy można wytworzyć im świat jednowymiarowy? Wracamy więc do przytoczonej na początku lokomotywy poruszającej się po prostym torze. Druty kwantowe wyobrazić sobie można jako bardzo cienkie paski wycięte z opisanej powyżej struktury BAB. Dwuwymiarowy ruch elektronu w warstwie A, przywołując wcześniejszy przykład z kanapką, to ruch wewnątrz bardzo cienkiego plasterka szynki. Jeśli kanapkę BAB pokroić na takie paseczki, których szerokość szynki będzie porównywalna z jej grubością, uzyskamy właśnie drut kwantowy. Jeśli szerokość, podobnie jak grubość, ma wymiar 100 Å, ruch w obydwu tych kierunkach jest niemożliwy. Jedynie wzdłuż drutu kwantowego elektron może poruszać się swobodnie. Wycinanie drutów kwantowych ze struktur dwuwymiarowych możliwe jest za pomocą dobrze zogniskowanej wiązki elektronowej. Cięcie takim nożem polega na niszczeniu przez wiązkę materiału i wytwarzaniu barier, do których elektrony nie mogą się przedostać. Jeśli wyobrazić sobie dwa cięcia wiązką elektronową w postaci linii równoległych do siebie i odległych o około 100 Å, to pozostaje pomiędzy nimi nienaruszony kryształ tworzący drut kwantowy.
Wreszcie można sobie wyobrazić, że druty kwantowe potniemy na kawałki. Jeśli wykorzystamy do tego jedną z wymienionych metod, np. dobrze zogniskowaną wiązkę elektronów, będziemy zdolni wycinać obszary, których i trzeci wymiar będzie rzędu 100 Å lub mniejszy. Elektrony znajdą się uwięzione w pudełku o bokach rzędu 100 A każdy, a zatem ruch w żadnym z tych trzech kierunków stanie się niemożliwy. W języku mechaniki kwantowej mówi się o elektronie (elektronach) zamkniętych w pudle. Takie kwantowo-mechaniczne pudło jest właśnie kropką kwantową. Z punktu widzenia ruchu swobodnego elektronu jest to układ zerowymiarowy, jako że w żadną stronę ruch wtedy nie jest możliwy. Okazuje się, że źródła światła zbudowane na bazie opisanych wyżej struktur, w gazach dwu-, a jeszcze lepiej w jedno-, czy zerowymiarowych
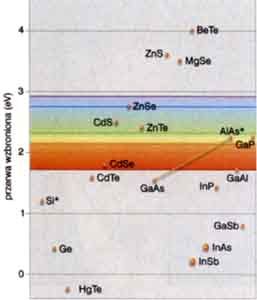
są bardziej wydajne niż w klasycznych gazach trójwymiarowych. Stąd też największe zainteresowanie budzą kropki kwantowe, które mogą stać sie najbardziej efektywnymi źródłami światła. Jednak zanim odpowiemy sobie na pytanie dlaczego tak jest zapoznamy się z kilkoma faktami z fizyki półprzewodników. W bardzo niskiej temperaturze bardzo czyste półprzewodniki (tzw.samoistne) prądu nie przewodzą. Elektrony (odpowiedzialne w metalach za przepływ prądu) znajdują się w stanach energetycznych tworzących całkowicie zapełnione pasmo (pasmo walencyjne), oddzielone obszarem niedostępnym energetycznie od pasma wzbudzonego, całkowicie pustego (pasmo przewodnictwa). Pasmo walencyjne i pasmo przewodnictwa to pasma dozwolone, natomiast obszar między nimi - to pasmo wzbronione, zwane też przerwą (elektronowi nie wolno mieć energii zawartej w tym paśmie). Półprzewodniki mogą mieć przerwę energetyczną, która równoważna jest energii kwantów światła z bardzo odległych zakresów widma.
Jeśli elektron z pasma walencyjnego zostanie w jakiś sposób wzbudzony do pasma przewodnictwa (dostarczona mu zostanie energia równa co najmniej wartości przerwy wzbronionej), może rozpocząć się przepływ prądu. Za przenoszenie ładunku, czyli przepływ prądu elektrycznego w półprzewodniku samoistnym, odpowiedzialne są nie tylko wzbudzone elektrony, ale i pozostawione przez nie "puste" miejsca w paśmie walencyjnym, które zachowują się jak cząstki dodatnio naładowane i noszą nazwę dziur. Przy tym samym znaku napięcia elektrycznego prąd dziurowy skierowany jest w przeciwną stronę niż prąd elektronowy.
Pobudzenie elektronu do pasma przewodnictwa może odbyć się albo wskutek podgrzania półprzewodnika, albo jego oświetlenia (pod warunkiem, że oświetlamy promieniowaniem o energii przewyższającej wartość przerwy wzbronionej). Wzbudzenie termiczne można ułatwić, domieszkując półprzewodnik, czyli wprowadzając niewielką ilość odpowiednio dobranych atomów chemicznie różnych od atomów macierzystego półprzewodnika. Wybór domieszki decyduje o tym, czy mamy do czynienia z obszarami bogatszymi w elektrony przewodnictwa (domieszkowanie donorowe), czy bogatszymi w dziury (domieszkowanie akceptorowe). Raz wzbudzony elektron może "zrekombinować" z dziurą, przy czym niekiedy towarzyszy temu wysłanie fotonu (im większa przerwa wzbroniona w półprzewodniku, tym krótsza może być długość fali świetlnej stowarzyszonej z takim wytworzonym w akcie rekombinacji promienistej fotonem), a niekiedy nadwyżka energii całkowicie zamienia się w ciepło. W półprzewodnikowych źródłach światła - diodach i laserach - ten ostatni proces jest oczywiście zjawiskiem niepożądanym.
Aby łatwiej zrozumieć, to co zostało wyżej napisane przytoczmy pewną analogię. Wyobraźmy sobie sieci rybackie zawieszone pionowo, rozpięte jedna nad drugą. W takim ujęciu rzeczy najwyższa sieć (oznaczmy ją numerem 1) jest pasmem przewodnictwa, ta pod nią to pasmo walencyjne (numer 2), a przestrzeń pomiędzy nimi to pasmo zabronione (przerwa). Pozostałe sieci (3, 4, 5, ...) nas nie interesują. Niech teraz piłki, czyli w naszym ujęciu - elektrony znajdują się na sieci nr 2 (dokładnie w okach sieci). Aby wzbudzić elektrony z pasma walencyjnego do pasma przewodnictwa należało im dostarczyć energię co najmniej równą Eprzerwa. W naszym kontekście należy przenieść piłkę z niższej sieci (nr 2) na wyższą (nr 1) wykonując przy tym pracę przeciwko grawitacji równą różnicy energii potencjalnej miedzy sieciami 1, a 2 (Esieć1 - Esieć2 = ΔE = Eprzerwa). Teraz sieć 1 jest częściowo zapełniona piłkami (elektronami) i może popłynąć prąd. Natomiast na sieci nr 2 pozostały puste miejsca po piłkach, które "czekają" na ich powrót (w półprzewodniku to miejsce nazywa się dziurą). Wiadomo, że stan najtrwalszy energetycznie to stan minimum energii potencjalnej i piłki będą dążyć do powrotu na niższą sieć nr 2 (będą spadać na nią i teraz pracę wykona siła grawitacji). Kiedy już piłce znudzi się przebywać na najwyższej sieci (nr 1), czyli wtedy, gdy jej równowaga zostaje zachwiana ( a piłka w naszym przypadku znajduje się w stanie równowagi nietrwałej - oka sieci są tak skonstruowane, iż piłka może się w nim utrzymać lub wypaść przez nie). Natomiast przestrzeń pomiędzy sieciami 1, 2 jest przezroczysta dla piłek. Analogiczna sytuacja jest w półprzewodniku, gdzie "spadaniu" elektronu z pasma przewodnictwa na pasmo walencyjne towarzyszy emisja kwantu promieniowania o energii nie niższej niż wielkość przerwy energetycznej. A co to wszystko ma do kropek kwantowych i ich wydajności świecenia? Powiedzmy najpierw czym jest foton, gdyż wielkości opisujące go mają kluczowe znaczenie do zrozumienia, dlaczego światło pochodzące z kropek kwantowych jest najintensywniejsze. Foton to cząstka, która jak każda cząstka posiada energię oraz pęd. Pęd fotonu jest bardzo mały, tak mały, iż w wielu rozważaniach po prostu przyjmuje się, iż jest on równy zeru (pęd fotonu to jego energia podzielona przez prędkość światła, czyli jego własną prędkość). Światło ma tak dużą prędkość, że pęd fotonu naprawdę z dobrym przybliżeniem można traktować jako zero. Energia fotonu jest wyrażona słynnym wzorem Einsteina E = mc2, gdzie m to masa relatywistyczna fotonu (masa spoczynkowa fotonu m0 wynosi zero). Jeśli elektron został pobudzony z niższego do wyższego stanu energetycznego i jakiś czas w tym wyższym stanie żyje, równie długo żyje miejsce po nim, czyli dziura, w niższym stanie energetycznym. Zarówno elektron, jak i dziura w czasie swojego żywota coś robią: poruszają się, zderzają z atomami albo defektami struktury (tzw. nieperiodycznościami potencjału). W wyniku tych wszystkich procesów elektron i dziura zmieniają swój pęd. Zmiana może być istotna, toteż po czasie życia w wyższym stanie energetycznym pęd elektronu i dziury znacznie różni się od pędu początkowego, jaki miały w chwili ich wytworzenia. I tu rozpoczyna się dramat: elektron chciałby spaść do czekającej nań dziury (rekombinować z nią), a różnicę energii wypromieniować w postaci fotonu.Jednak w każdym procesie fizycznym spełnione muszą być - prawo zachowania energii i prawo zachowania pędu. Pierwsze mówi, że suma energii przed i po procesie musi być taka sama (energia musi być zachowana). Z jego spełnieniem nie ma większych kłopotów, bo emitowany foton zabiera różnicę energii. Należy tutaj dodać, że kiedy elektron, który przeszedł do pasma przewodnictwa i w wyniku zderzeń uzyskuje dodatkową energię, to przechodzi on na ściśle określony wyższy podpoziom pasma przewodnictwa, z których to pasmo jest złożone (czyli tak jakby sieć nr 1 była pewnym układem złożonym z wielu podsieci gęściej ułożonych niż sieci główne). Prawdziwy kłopot jest ze spełnieniem prawa zachowania pędu, które mówi, że suma pędów układu przed procesem i po procesie musi być taka sama. Jeśli w czasie swojego żywota elektron i dziura uzyskały jakieś pędy, to po rekombinacji ich suma powinna być taka sama. Jednak tutaj sprawa się nieco komplikuje, gdyż że pęd jest wielkością wektorową - oprócz wielkości ma również zwrot i kierunek. Innymi słowy - należy go rozłożyć na trzy składowe (jeśli proces zachodzi w świecie trójwymiarowym) i prawo zachowania pędów musi być spełnione dla każdego z tych kierunków. Możemy, jak poprzednio, próbować wszystko "zwalić" na emitowany foton: niech zabierze nadmiar pędu i doprowadzi do spełnienia wymaganego prawa. I tu znowu jest kłopot: foton nie może zabrać (ani dostarczyć) pędu, który powinien być zabrany. Zatem za pomocą cząstek, które mamy do dyspozycji, nie udaje się spełnić trzech równań (dla różnych kierunków składowych) wynikających z prawa zachowania pędu. Rekombinować i wyświecać fotony mogą więc tylko te elektrony i dziury, dla których prawo zachowania pędu jest spełnione. Ale takich par elektron-dziura jest bardzo mało, a zatem liczba procesów, które mogą zachodzić, decydując o intensywności wypromieniowanych fotonów, jest też mała. Czy istnieje jakieś wyjście z tej kłopotliwej sytuacji? Okazuje się, że najprościej byłoby zamienić świat trójwymiarowy na dwuwymiarowy. Jeśli elektrony i dziury będą mogły się poruszać tylko w dwóch kierunkach będą mieć dwie składowe pędu zamiast trzech, do spełnienia pozostaną więc dwa równania wynikające z prawa zachowania pędu. Wtedy rekombinacja elektronów i dziur będzie znacznie bardziej prawdopodobna i emisja fotonów bardziej intensywna. Teraz widać już dlaczego należy budować opisywane struktury.Okazuje się, że natężenie fotonów emitowane z diody elektroluminescencyjnej, w której elektrony są dwuwymiarowe (podobnie jak dziury), znacznie przewyższa to, co moglibyśmy otrzymać z takiej diody wykorzystującej elektrony i dziury trójwymiarowe. 
Rys.3. Obraz rzeczywistych kropek "naciętych" na dwuwymiarowej strukturze Zatem emisja światła w następstwie rekombinacji zerowymiarowych elektronów i dziur powinna być ogromna. I tędy prowadzi droga do bardzo wydajnych źródeł światła. Pójdźmy zatem jeszcze dalej: jeśli elektrony i dziury nie będą mogły w ogóle się poruszać, czyli ograniczymy ich ruch we wszystkich trzech kierunkach, ze spełnieniem prawa zachowania pędu nie będzie już żadnych problemów. Zatem emisja światła w następstwie rekombinacji zerowymiarowych elektronów i dziur powinna być ogromna. I tędy prowadzi droga do bardzo wydajnych źródeł światła.Z przedstawionego rozumowania wynika, że zjawiska zachodzące w kropce kwantowej są, z punktu widzenia efektywności świecenia, bardziej wydajne niż np. w gazie dwuwymiarowym. Jest jednak problem, który działa niekorzystnie, a mianowicie lokalizacja elektronów i dziur. Jeśli mają znajdować się wewnątrz kropki kwantowej, efekt ten może być znaczący i nie należy go zaniedbywać. Wyjątkowe możliwości badawcze i aplikacyjne stwarza odkrycie kropek kwantowych. Szczególnie interesującą sytuację uzyskuje się umieszczając w procesie produkcji elektrodę zwaną bramką wokół kropki. Zwiększenie potencjału elektrycznego bramki zmniejsza rozmiary kropki. Zwiększenie potencjału elektrycznego bramki zmniejsza rozmiary kropki, "ściskając" elektrony i powodując wzrost energii stanów elektronowych w kropce. Jeżeli jeszcze dodać w otoczeniu kropki elektrody, które mogą służyć jako kontakty dla elektronów tunelujących do wnętrza kropki lub na zewnątrz niej, otrzymujemy strojoną kropkę kwantową. W przypadku takiej kropki możemy regulować jej kształt oraz liczbę znajdujących się w niej elektronów. W rezultacie otrzymujemy coś co można nazwać sztucznym atomem dającym się modyfikować pod względem kształtu i liczby elektronów za pomocą potencjałów bramki i elektrod (lokalizujący potencjał bramki działa jak przyciągające jądro). Jeszcze bardziej fascynujące możliwości uzyskuje się wytwarzając duże, periodyczne sieci kropek kwantowych (konstruując bramkę w postaci elektrody siatkowej). Taka sieć jest rodzajem warstwy sztucznego kryształu zbudowanego ze sztucznych atomów. Za pomocą zmian napięcia przykładanego do elektrody siatkowej można regulować i kontrolować własności poszczególnych "atomów" (rozmiary kropek i liczbę znajdujących się w nich elektronów), a także własności całego "kryształu" regulując odległości między "atomami" (wysokość i szerokość bariery pomiędzy kropkami). |